Análisis de Estabilidad de Sistemas Materiales Parte I: teoría y caso práctico
Todas las publicaciones sobre Estática Aplicada se han recopilado en el siguiente enlace:
•Material para Estática Aplicada
Saludos y bienvenidos, luego de un periodo de tiempo de poca actividad en Steemit motivado a compromisos académicos en la universidad, por lo cual debo ponerme al día, vamos a retomar el estudio de la estática aplicada con el tema del análisis de la estabilidad de sistemas materiales mediante el teorema de Kennedy (o teoremas de los polos), se buscará con la presente publicación explicar de forma didáctica y detallada el estudio de la estabilidad de sistemas materiales mediante métodos analíticos, gráficos y teóricos. Es importante para el estudiante de Ingeniería Civil aprender a analizar los distintos sistemas estructurales y discernir en su estado de estabilidad ya sea observando la manera en que están dispuestas las vinculaciones (o la cantidad de ellas) o realizando un análisis geométrico-gráfico del mismo para verificar si el sistema es o no inestable. Especial saludo a la comunidad de #STEM-espanol con la cual se comparte y se aprende valioso conocimiento científico y académico.
Introducción
Los grados de libertad de un sistema material señalan cuantos parámetros de movimiento independientes (desplazamientos o rotaciones) posee el sistema, se pueden calcular mediante la Ecuación (3) del artículo Determinación Algebraica de los Grados de Libertad de Sistemas Materiales en Estática Aplicada y Ejemplo de Aplicación:
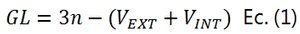
Donde “n” representa el número de chapas, “Vext” y “Vint” la cantidad de unidades de vinculación externas e internas respectivamente. Esta ecuación nos indica el grado de estabilidad que puede tener un sistema material, los cuales son: GL<0 (hiperestático, exceso de vinculaciones), GL=0 (isostático), o GL≥1 (hipostático, mecanismo inestable).
Si se puede establecer el grado de estabilidad de un sistema material mediante la ecuación (1), entonces ¿Por qué realizar un análisis adicional?
Recordemos que pueden existir vinculaciones mal dispuestas (vínculos aparentes) que no están introduciendo restricción alguna al sistema y pueden estar generando inestabilidad. Esto no es tomado en cuenta por la Ecuación (1), ya que totaliza todas y cada una de las vinculaciones sin importar su disposición en el sistema material. Es por ello que se dice que para que un sistema sea estable, la condición GL=0 es necesaria pero no suficiente, ya que la ecuación deja de ser válida si existen vínculos aparentes.
Debido a lo anteriormente expuesto, un sistema material el cual posee cero grados de libertad de acuerdo a la ecuación (1) no puede ser clasificado directamente como “isostático” o “estable”, ya que pueden existir uno o más vínculos aparentes que conviertan el sistema en un mecanismo inestable.
Existen vinculaciones aparentes que mediante una simple inspección visual presentan relativa sencillez para ser identificadas, pero en algunas ocasiones no son tan evidentes a simple vista. Aquí es donde entra en juego el teorema de los polos (Teorema de Kennedy), el cual nos permite identificar cuando una vinculación está de sobra en el sistema material.
Este teorema se basa en lo siguiente: para que un sistema posea un grado de libertad (GL=1), debe existir un alineamiento entre los polos de las chapas que conforman dicho sistema. De esta manera, podemos aplicar este teorema en el análisis de estabilidad para verificar lo que la Ecuación (1) nos proporciona. El cumplimiento de este teorema en su totalidad o solo en ciertas partes de un sistema material ya nos indica que existe inestabilidad en el mismo.
Los Vínculos y sus Polos
Recordando un poco lo que caracteriza el movimiento de una chapa en el plano, tenemos que el desplazamiento de un punto cualquiera de una chapa será perpendicular al radio vector que une el polo de dicha chapa con el punto en cuestión. Al ser movimientos infinitésimos los que puede presentar una estructura en la realidad, en estática aplicada se asumirá que la rotación “φ” que puede presentar una chapa en un instante dado es de orden infinitesimal, por lo tanto podemos asumir Tan(φ)=φ. Además se asume que el polo absoluto no cambia de posición y será un punto fijo.
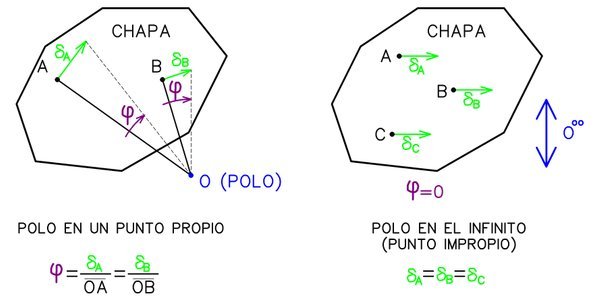
Un caso particular se presenta cuando todos desplazamientos de los puntos de una chapa son paralelos y de igual magnitud ya que la chapa no presenta rotación y está en traslación pura. En este caso se asume que el polo absoluto se encuentra en el infinito (punto impropio).
Como se ha observado, el movimiento de una chapa viene dado por la ubicación de su polo, y este a su vez depende de la restricción que aporten las vinculaciones sobre la misma. Cada vínculo nos proporciona información útil acerca de la ubicación del polo de la chapa a la cual vincula. Los vínculos externos restringen la ubicación del polo absoluto de una chapa, mientras que los vínculos internos brindan información acerca de la ubicación del polo relativo entre las chapas a las cuales vincula. Los polos absolutos indican cómo es el movimiento de una chapa respecto al sistema tierra, mientras que los relativos muestran como es el movimiento de una chapa respecto a la otra.
Tomando en cuenta la descripción de los vínculos que se dio en el artículo Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad, podemos decir que:
- Los vínculos de primer grado brindan información acerca de la dirección del polo o directamente nos brindan su ubicación en el infinito (más no la dirección). Nunca nos dan toda la información acerca del polo absoluto/relativo por sí solos.
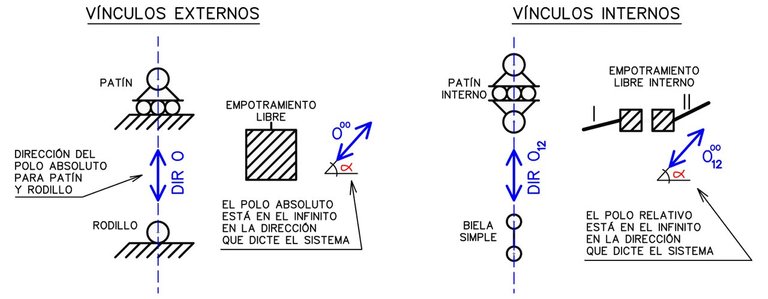
- Los vínculos de segundo orden nos dicen directamente dónde se encuentra el polo absoluto/relativo. El mismo puede ser un punto fijo (punto propio) o encontrarse en el infinito (punto impropio).
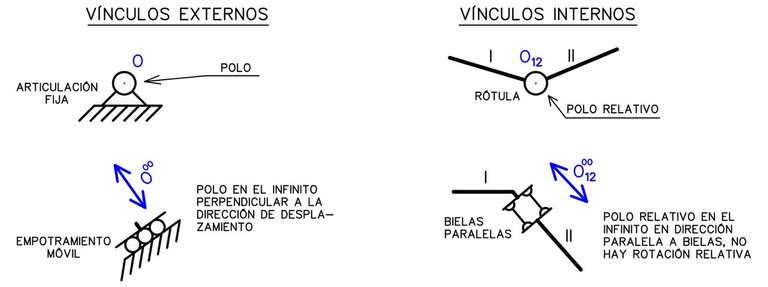
- Los vínculos de tercer orden no permiten ningún movimiento ya sea respecto al sistema tierra o respecto a otra chapa. Si no hay movimiento, no existen centros de rotación, y por lo tanto no existen los polos.
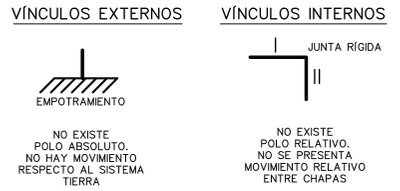
Teorema de Kennedy (Teoremas de los Polos)
El teorema de Kennedy se basa en el estudio de los centros instantáneos de rotación de mecanismos y es utilizado en estudios de Mecánica Aplicada. En estática aplicada se le conoce como “teoremas de los polos”. Antes de entrar en los teoremas de los polos, veremos primero lo que son las cadenas cinemáticas.
Cadenas Cinemáticas
Según Rodríguez (2003), las cadenas cinemáticas se pueden definir como: ”Conjunto material plano formado chapas rígidas conectadas por vínculos de segundo grado. Se clasifican en cadenas cinemáticas abiertas y cadenas cinemáticas cerradas”. (p. 25). De esta manera podemos denominar a cualquier sistema de chapas vinculadas entre sí por vínculos de segundo orden como cadena cinemática, la cual será abierta, cerrada, o poseer ambas características.
Cadenas Cinemáticas Abiertas
Son sistemas materiales cuyas chapas son contiguas entre sí creando una figura abierta. Representan mecanismos cinemáticos de 1 o más grados de libertad.
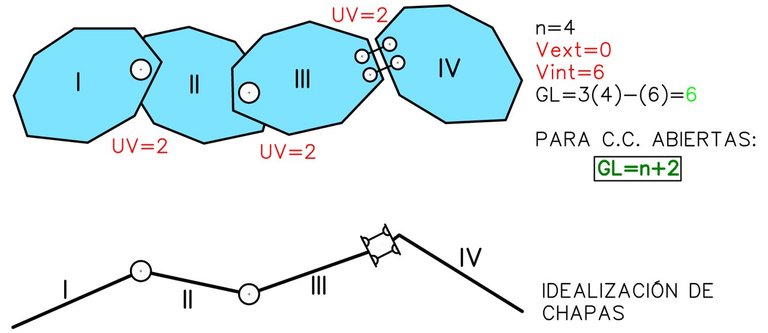
Cadenas Cinemáticas Cerradas
Representan mecanismos cuyas chapas están vinculadas entre sí formando un “circuito”.
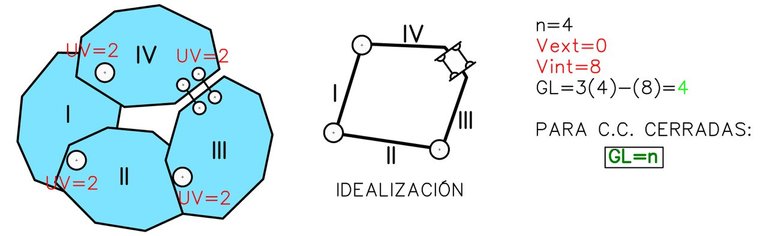
Un sistema material puede ser la combinación de cadenas cinemáticas abiertas y cerradas.
Cadenas Cinemáticas de 1 Grado de Libertad
Son sistemas materiales que poseen una forma única de moverse, en otras palabras poseen un solo parámetro de movimiento independiente. Cada chapa tiene solo un movimiento posible, y los movimientos de todos los puntos del sistema pueden expresarse en función de un solo parámetro (por ejemplo, en función de una rotación “α” que se le asigne a una de las chapas). Cuando se cumple que GL=1, se puede efectuar el “análisis por movimiento infinitésimo” al sistema material, el cual resulta de dar a una de las chapas un desplazamiento o rotación arbitraria y expresar todos los desplazamientos de los puntos del sistema y las rotaciones de todas las chapas en función de este valor arbitrario.
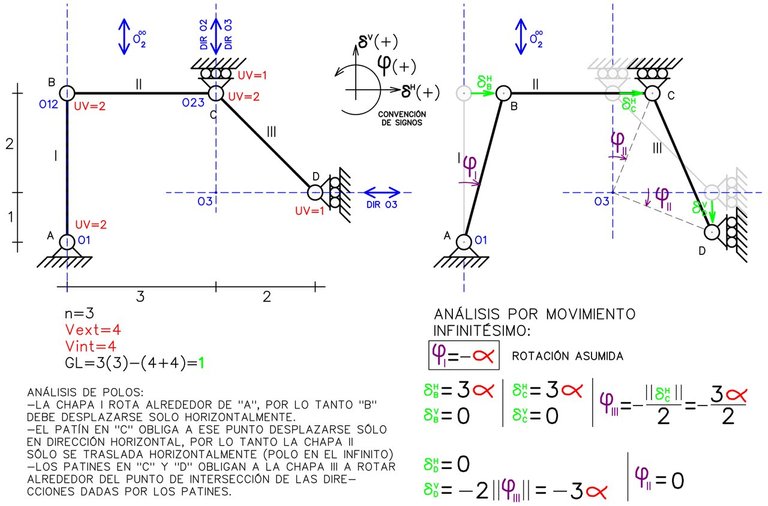
Los teoremas de los polos se fundamentan sobre estos sistemas tal como veremos más adelante.
Primer Teorema de los Polos
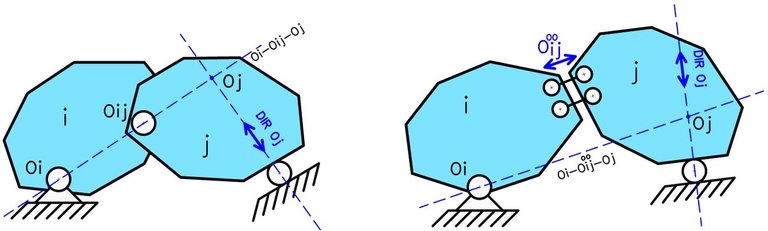
Este teorema se basa en los polos absolutos. Hernández (1998), señala que: “En un mecanismo cinemático de un grado de libertad, los polos absolutos de dos chapas cualesquiera se encuentran alineados con el polo relativo entre ellas”. (p. 24). De esta manera, si se cumple este teorema entre dos chapas vinculadas entre sí, estamos en presencia de un mecanismo cinemático de un grado de libertad formado por estas dos chapas.
Sea una chapa “i” y otra “j”, el 1mer TDP se cumplirá si:
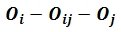
Es decir, se alinean el polo relativo con el polo absoluto de ambas chapas. Un ejemplo de esto se puede representar con el siguiente sistema material.
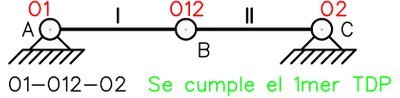
Podemos ver que perfectamente existe alineamiento entre ambos polos absolutos con el relativo, esto indica que el sistema mostrado es un mecanismo cinemático de 1 grado de libertad, tal como lo indica el teorema. El mecanismo viene dado por el posible desplazamiento vertical (infinitesimal) del punto B. Si aplicamos la ecuación (1) a este sistema encontramos que llegamos a la condición GL=0, el sistema tendría las vinculaciones suficientes para ser estable, pero al estar mal dispuestas se genera un mecanismo inestable. Esto indica que el 1mer TDP puede cumplirse independientemente del número de vinculaciones existente, si están mal dispuestas se generará un mecanismo cinemático. Sin modificar el número de chapas y vinculaciones podemos convertir este mecanismo en un sistema estable (Fig. N°11).
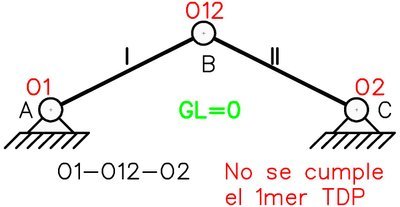
Observamos ahora que no hay alineamiento de polos, por lo que el sistema tendría 0 grados de libertad tal como lo indica la ecuación (1). Este sistema estable se conoce como “arco triarticulado”.
Podemos decir que la estabilidad no depende solo del número de vinculaciones disponibles, sino de la geometría del sistema y de la manera en que están dispuestas estas vinculaciones.
Veamos otro ejemplo de como la geometría del sistema y la disposición de los vínculos marcan la diferencia entre la estabilidad y la inestabilidad.
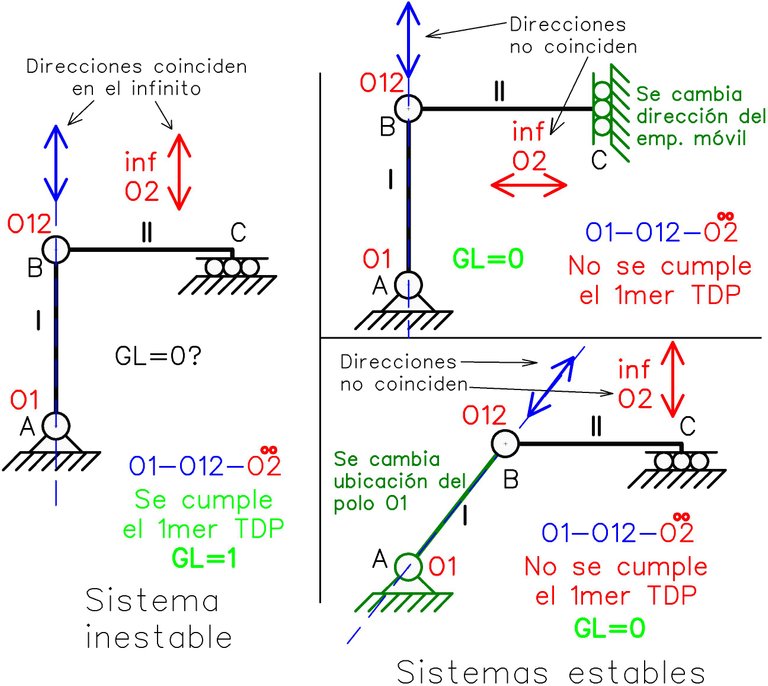
Se ha verificado como modificando la disposición de uno de los vínculos (empotramiento móvil) o cambiando la geometría se puede convertir un sistema inestable en estable siempre y cuando este tenga el número suficiente de vinculaciones (GL<0), de lo contrario se deberán agregar vinculaciones para llegar a la estabilidad (caso GL>0).
Existen distintas formas en las que puede cumplirse del 1mer TDP. La siguiente ilustración especifica cada una de ellas, en donde todos los sistemas mostrados poseen 1 grado de libertad.
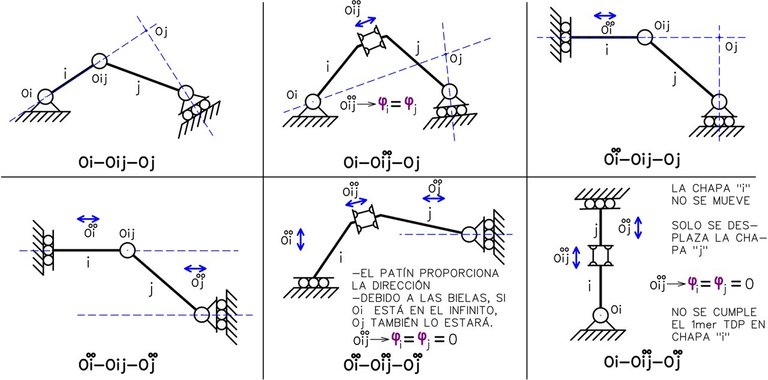
Las variaciones en el cumplimiento del 1mer TDP se dan debido a que todos o algunos de los polos involucrados está en el infinito (punto impropio) y es importante reconocer cada caso en el análisis de estabilidad. Especial atención debe ponerse al último caso, donde existe un polo absoluto ubicado en un punto propio y los dos polos restantes en el infinito, esto indica que la chapa cuyo polo no está en el infinito no podrá moverse, debido a que las bielas imponen la condición de que la rotación es igual para ambas chapas (si la chapa “i” no rota, entonces “j” tampoco, y “j” no puede desplazarse).
Segundo Teorema de los Polos
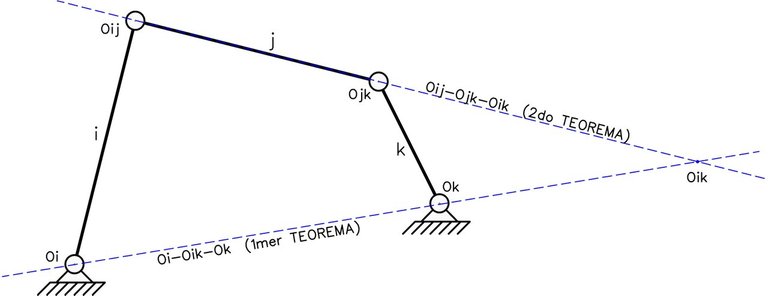
Basado en los polos relativos. De acuerdo a Hernández (1998): “En un mecanismo cinemático de un grado de libertad los polos relativos entre tres chapas cualesquiera se encuentran alineados”. (p. 24). Este teorema suele ser poco abordado en estática aplicada pero es igual de válido que el primero.
El 2do TDP se cumplirá al presentarse la siguiente alineación de polos relativos entre tres chapas “i”, “j” y “k”:
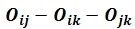
El orden de los polos relativos no incide en el cumplimiento de este teorema.
Cabe destacar que aunque dos de las tres chapas del sistema mostrado en la Fig. N°14 no se encuentren en contacto directo, existe un polo relativo entre ellas, y representa un punto en el cual existiría una articulación si ambas chapas se extendieran hasta el mismo (Fig. N°15).
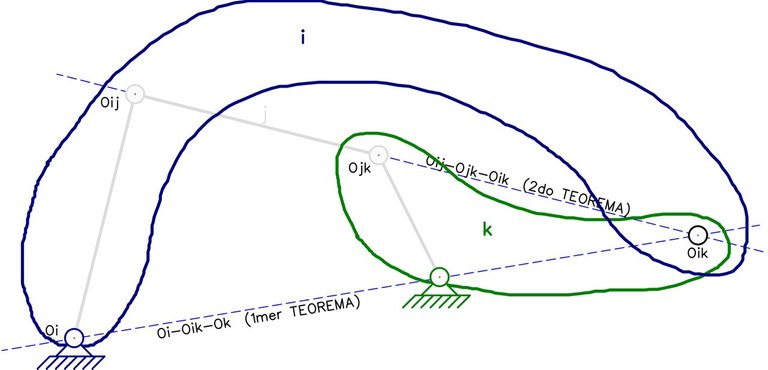
La aplicación de este teorema no es estrictamente necesaria, ya que es suficiente con aplicar el 1mer TDP para realizar el análisis de estabilidad.
Análisis de Estabilidad de Sistemas Materiales
Podemos definir “estable” como el estado en el que un sistema material o chapa no puede moverse. Esto se da cuando se verifica que GL≤0 o cuando una chapa posee más de una solución para la ubicación de su polo absoluto, recordando que es imposible que un punto material rote alrededor de dos centros de rotación al mismo tiempo.
La finalidad de estudiar y conocer los teoremas de los polos es la de verificar su cumplimiento en el sistema material, ya que esto indica la presencia de mecanismos inestables dentro del mismo. De esta forma, analizar la estabilidad de un sistema material implica verificar que no se cumple el 1mer TDP. Para ello se sigue la siguiente metodología:
1) Se calculan los grados de libertad de acuerdo a la ecuación (1).
2) Se ubican los posibles polos absolutos y relativos que tendría el sistema de acuerdo a la vinculación existente.
Es posible que luego del paso N°2 se pueda concluir directamente que alguna de las chapas del sistema sea estable debido a que los vínculos sobre ella brinden más de una solución para su polo absoluto.
3) Se aplica el 1mer TDP para obtener las posibles ubicaciones de los polos aún desconocidos. Es posible que los vínculos por si solos no aporten información suficiente para hallar la totalidad de los polos absolutos y relativos en el sistema.
Luego de realizar el paso N°3 se debe analizar si se cumple el 1mer TDP en la totalidad o parte del sistema y descartar la existencia de vínculos aparentes. En total pueden presentarse 3 situaciones:
La primera implica que se cumple el 1mer TDP entre cada una de las chapas del sistema, o parcialmente (siendo el resto estable). Se concluye que GL=1.
La segunda implica que no se ha cumplido el 1mer TDP en el sistema, indicando que ninguna chapa se mueve, siendo el sistema estable en su totalidad (GL≤0).
La tercera situación, la cual es menos común, implica que aún realizado todos los pasos no se ha podido hallar el polo absoluto de una o más chapas del sistema (o el polo relativo entre chapas), es decir, no se posee la información suficiente para establecer la ubicación del mismo. Esto indica que la ubicación del polo no puede ser definida pues el sistema presenta más de una forma de moverse (mecanismo de varios grados de libertad). Se concluye que GL>1.
A través del siguiente ejemplo pondremos en práctica lo antes expuesto.
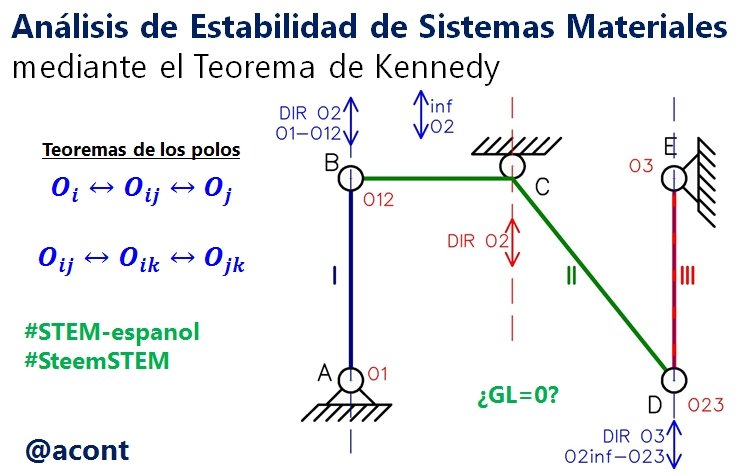
Ejemplo: estudiar la estabilidad del siguiente sistema material. De existir algún vínculo aparente, indicar su ubicación.
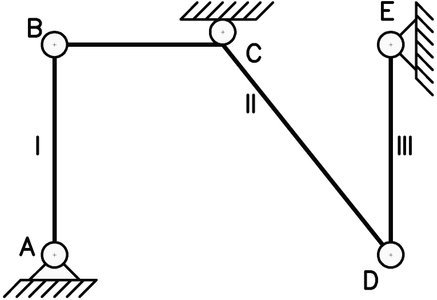
Tenemos un sistema material con un total de 3 chapas. 5 unidades de vinculación externas (2 por cada articulación a tierra y 1 por el apoyo simple). 4 unidades de vinculación internas (2 en cada rótula).
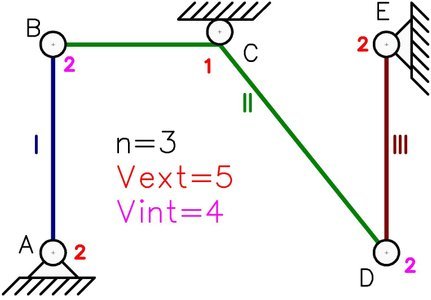
Al aplicar la ecuación (1) obtenemos:
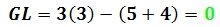
Este resultado debe ser verificado mediante un análisis geométrico del sistema para descartar la existencia de vínculos aparentes.
Primero hallamos los polos que tendría el sistema de acuerdo a las restricciones que aportan los vínculos existentes. Las articulaciones a tierra brindan directamente la ubicación de los polos absolutos de I y III, así como las rótulas la de los polos relativos O12 y O23. El apoyo simple en C brinda una dirección sobre la cual se encontraría el polo O2.
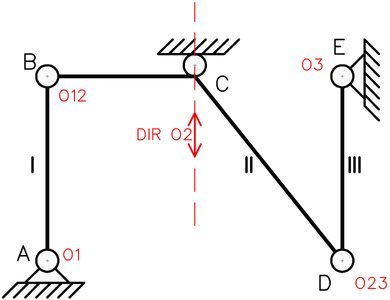
Se observa que aún no se conoce la ubicación del polo absoluto O2, para ello empezaremos a aplicar el 1mer TDP (paso N°2). Si el 1mer TDP se cumple, el polo O2 debe de estar alineado con O1 y O12, por lo que se traza una dirección que pasa por estos. La ubicación del polo O2 se encontraría en la intersección de las direcciones:
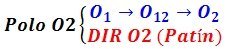
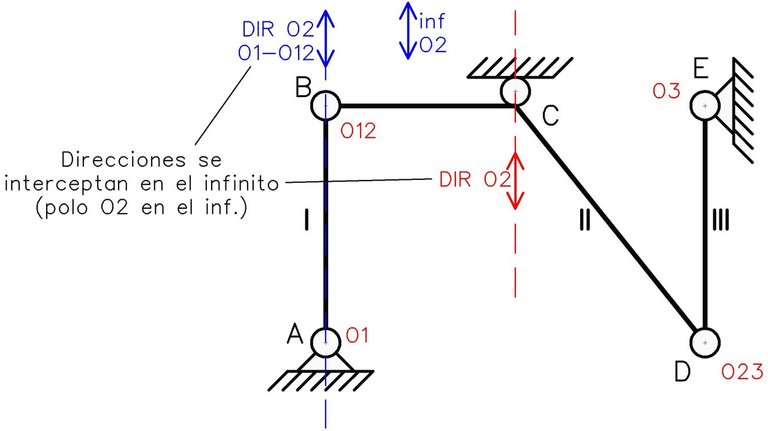
Esta dirección trazada mediante el 1mer TDP se intercepta con la dirección dada por el apoyo simple C en el infinito ya que son paralelas. Como resultado el polo O2 se encuentra en el infinito (punto impropio), indicando que la chapa II se estaría desplazando horizontalmente. Hasta ahora, al no existir otra solución para el polo O2, se estaría cumpliendo el 1mer TDP entre I y II.
Seguidamente comprobaremos si se cumple el 1mer TDP entre II y III. Para ello se traza a través del polo relativo propio (O23) una dirección paralela a la dirección que tiene O2 hacia el infinito.
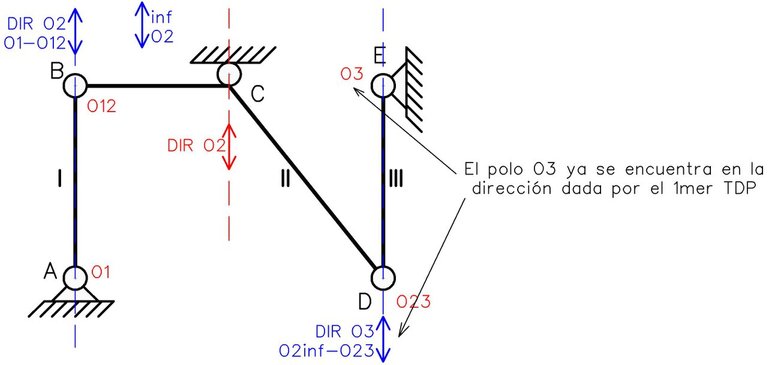
Se observa que el polo O3 (el cual ya se había hallado anteriormente por las restricciones de vínculo) coincide con esta dirección dada por el 1mer TDP. Por lo que se está cumpliendo el teorema en todo el sistema:
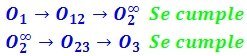
De acuerdo a lo visto anteriormente, debido al cumplimiento del 1mer TDP, el sistema posee 1 grado de libertad. Ya que la ecuación (1) resultó en 0, estamos ante la presencia de un vínculo aparente, el cual es tomado en cuenta por la ecuación (1) y no está aportando restricción alguna al sistema.
La manera de identificar el vínculo aparente es observando la redundancia que se genera al verificar el cumplimiento del 1mer TDP. Vemos que el polo O3 ya se encuentra en la dirección dada por el teorema, sin embargo, si no conociéramos la ubicación de este polo, bastaría con conocer otra dirección para hallar su ubicación (tal como se halló el polo absoluto de la chapa II). En efecto, podemos eliminar una de las restricciones de la articulación fija en E, convirtiendo ese vínculo en un apoyo móvil que solo proporcione una dirección para la ubicación del polo absoluto.

Tal como se observa, la ubicación del polo O3 no se ve afectada al remover esta vinculación, ni tampoco la de otros polos. Esta restricción eliminada, que no altera el comportamiento del sistema, representa el vínculo aparente.
En conclusión, el sistema material posee 1 grado de libertad y se halló 1 vinculación aparente.
Ahora, surgen una serie de preguntas:
*¿Existe una solución única para el vínculo aparente?*
No, debido a que al ejecutar este mismo análisis pero empezando desde el punto E nos encontramos que esta vez la restricción vertical de A representa al vínculo aparente. La ubicación del vínculo aparente depende de donde se empiece a ejecutar el análisis de estabilidad. Se puede observar que sin esta restricción, la ubicación de los polos tampoco se ve afectada. La solución debe ser única, en este caso debe establecerse si se va a eliminar la restricción vertical de E o la de A, eliminar ambas simultáneamente alteraría el comportamiento del sistema.
*¿La existencia del vínculo aparente depende de la geometría del sistema?*
Si, se puede observar que con solo modificar la forma en que están dispuestas las vinculaciones o las chapas, podemos evitar la alineación de polos entre chapas impidiendo así el cumplimiento del primer teorema de los polos. Ya sea modificando la orientación del “patín” (girándolo noventa grados) o desplazando horizontalmente alguna de las dos articulaciones fijas (A o E), podemos asegurar la estabilidad del sistema y la no existencia de un vínculo aparente.
*¿Qué hay del segundo teorema de los polos?*
La comprobación del cumplimiento del 2do TDP no es estrictamente necesaria, siendo suficiente analizar el sistema para comprobar si se cumple o no el 1mer TDP. En el ejemplo mostrado podemos comprobar el cumplimiento de este teorema verificando si existe alineamiento entre los polos relativos de las tres chapas. Para ello se debe hallar el polo relativo O13. Se sabe por el 2do TDP que debe existir el siguiente alineamiento:
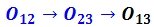
Pero solo una dirección no es suficiente, por lo que se debe recurrir al 1mer TDP para obtener otra. Debe de cumplirse también entre las chapas I y III:
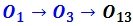
Obteniendo así la ubicación del polo relativo desconocido:
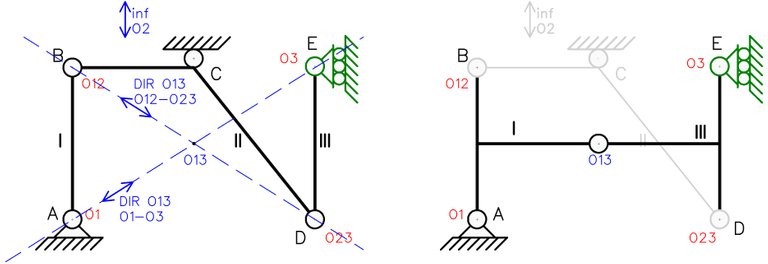
Al no existir alguna otra solución para el polo relativo O13 se da por verificado el cumplimiento del 2do TDP.
¿Qué se puede concluir hasta ahora?
- El teorema de Kennedy (o teorema de los polos), es una herramienta que permite estudiar mediante un método gráfico-analítico la estabilidad de sistemas materiales en el plano.
- Se establece la posibilidad de utilizar un teorema usado comúnmente en la mecánica aplicada para analizar sistemas materiales en estática aplicada desde el punto de vista de la estabilidad.
- El teorema de Kennedy permite verificar el resultado de la ecuación utilizada para calcular los grados de libertad, ya que la misma no puede distinguir, o visto de otra manera, no toma en cuenta la forma en que están dispuestas las vinculaciones en el sistema, generando inestabilidades aún si se cuenta con el número suficiente de unidades de vinculación para poder garantizar la estabilidad.
- Se pueden hallar vínculos aparentes en sistemas materiales mediante el teorema de Kennedy, al verificar que existe redundancia entre la vinculación existente y las direcciones proporcionadas por el primer teorema de los polos (parte del teorema de Kennedy).
- Para el estudiante de Ingeniería Civil es importante aprender a reconocer la estabilidad y la posible inestabilidad de una estructura, por ello en el estudio de la Estática Aplicada se hace énfasis en analizar la estabilidad de sistemas materiales.
En las próximas publicaciones abordaremos distintos casos de sistemas materiales que incluyen otras vinculaciones las cuales pueden presentar un desafío diferente a la hora de analizar la estabilidad así como también diferentes formas en las que el vínculo aparente puede presentarse.
Referencias Bibliográficas
Rodríguez, Iván. (2003). Estática de las Estructuras.
Hernández, Suilio. (1998). Estática Aplicada. Folleto Editado por el Departamento de Ingeniería Estructural U.C.V. Caracas.
Lecturas recomendadas
Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad
Criterios de Estabilidad de Sistemas Materiales en Estática Aplicada
Imágenes y ecuaciones de autoría propia realizadas mediante LibreCAD y Microsoft Word por @acont.
Toda una clase magistral la que nos brindas en esta publicación estimado @acont, en lo referente al teorema de polos. Recuerdo que en mis inicios del postgrado de Ingeniería Sismorresistente en la Universidad Central de Venezuela, específicamente en el curso de Introducción a la Dinámica de Estructuras, confirmé lo importante de tener claro estos conocimientos. Este artículo es una referencia muy didáctica para adentrarse al estudio de la estabilidad de las estructuras, de gran utilidad tanto para estudiantes de ingeniería civil como para profesionales que se desenvuelven en el mundo del cálculo estructural. Excelente publicación compañero @acont, felicidades y bendiciones!
Gracias estimado colega @eliaschess333 tal como acotas es importante reconocer la estabilidad de un sistema estructural, como mencionas en la Dinámica de Estructuras existe la posibilidad de presentarse inestabilidad debido a movimientos sísmicos y al ser estructuras lo que se analiza, se asumen hipótesis restrictivas para cada uno de los miembros (área o inercia infinita) ya que tal como lo define Luchsinger C. (1976): "Una estructura es una cadena elástica estable, compuesta por un número finito de miembros...". (p.6). En Estática al estudiar cuerpos rígidos se asumen tanto áreas como inercias infinitas y la inestabilidad se presenta por ausencia o mala disposición de vínculos. Saludos!
Fuente: Luchsinger C. (1976). Estructuras (Tomo I). Folleto editado por el Departamento de Ingeniería Estructural U.C.V. Caracas.
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @utopian-io.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness and utopian-io witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having added @steemstem as a beneficiary to your post. This granted you a stronger support from SteemSTEM.
Thanks for having used the steemstem.io app. You got a stronger support!
Thanks for the support!
Congratulations @acont!
Your post was mentioned in the Steem Hit Parade for newcomers in the following categories:
I also upvoted your post to increase its reward
If you like my work to promote newcomers and give them more visibility on the Steem blockchain, consider to vote for my witness!
Thank you for the mention.
You're welcome @acont. I'm glad to help.
BTW, feel free to vote for me as a witness if you like my work at promoting newcomers

Posted with
Hi @acont!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Thanks! @utopian-io
Congratulations @acont! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!