Recuperé algunos apuntes de Matemáticas relacionado con el cálculo binomial, también tiene que ver con mi última publicación sobre Desarrollo del cálculo binomial para hallar el área de una figura geométrica, así que seguiré tratando el tema de binomios, específicamente la multiplicación de 2 binomios.

Ya lo vimos anteriormente, la multiplicación de 2 binomios puede dar como resultado un trinomio o un cuatrinomio

Ahora veremos un caso particular donde los 2 binomios no tienen términos aleatorios, sino que presentan 1 témino en común. Veamos el siguiente ejemplo:

El producto no tiene nada en particular, esto es algún término que los relacione, ya que el grado del polinomio es 7 y disminuye hasta 4 en este cuatrinomio. Veamos qué sucede al colocar el segundo término del mismo grado:

(5X² + 2X³)×(5X² + 3X³) =
= (5×5)(X²×X²) + (5×3)(X²×X³) + (2×5)(X³×X²) + (2×3)(X³×X³) =
= 25X⁴ + 15X⁵ + 10X⁵ + 6X⁶
= 25X⁴ + 25X⁵ + 6X⁶
La multiplicación de 2 binomios va formando un patrón que relaciona sus términos, el primer término del producto es el cuadrado del término en común de los 2 binomios, mientras que el tercer término del producto es el resultado de multiplicar los 2 segundos términos de los binomios. También es interesante notar que el producto de estos 2 binomios es un trinomio

Hagámoslo más simple (por donde debimos haber comenzado), proponiendo el cálculo binomial con términos numéricos:

Lógica matemática:

sin duda, ya lo tenemos resuelto: el primer término del producto (trinomio) es el cuadrado del término en común de los 2 binomios, el tercer término del trinomio es la multiplicación entre los segundos términos de los binomios y se deduce matemáticamente que el segundo término del trinomio es el producto de la suma de estos segundos términos por el término en común de los binomios.

Podemos plantear la multiplicación de 2 binomios que tengan 1 término en común y el segundo término del mismo grado o un coeficiente numérico, mediante la siguiente expresión:

El cálculo binomial para hallar el área de un rectángulo

La expresión matemática que se ha planteado, corresponde a un Producto Notable, el cual puede ser utilizado en el cálculo del área de una figura geométrica, el rectángulo.

Los lados de este rectángulo son: (M + x) y (M + y). Note que tienen la forma de un binomio, con M como término común, además se tiene la desigualdad x ≠ y

El procedimiento para la determinación del área de un rectángulo de lados desiguales (por supuesto), se basa en el cálculo binomial del producto de 2 binomios con 1 término en común, en este caso M.

Sumando el cuadrado interno más los 3 rectángulos internos, dan como resultado el área total del rectángulo de lados (M + x) y (M + y).

Usemos unidades métricas:

Calculemos el área de un rectángulo cuyas medidas son: M = 1 cm, x = 0,3 cm con y = 0,5 cm.

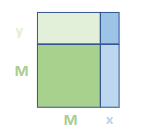
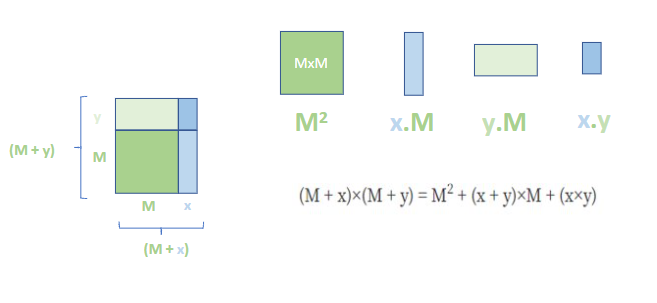
El área total del rectángulo se obtiene del cálculo binomial como la sumatoria de las figuras geométricas internas, teniendo presente el producto notable presentado en el cuerpo del manuscrito.

Para finalizar, podemos determinar los términos y factores que conforman el producto de 2 binomios con un término en común a partir del trinomio que se nos presente, siempre y cuando cumpla con los 2 criterios mencionados anteriormente. Veamos el siguiente ejemplo: a partir de la expresión (M² + 4M − 60), determine los 2 binomios originales.

Debemos tener presente que la expresión del producto de 2 binomios es:

(M + x)×(M + y) = M² + (x + y)×M + (x × y)

de tal manera que el término en común es M, el primer término del trinomio, cuyo exponente es 2. Luego, (x + y) = 4 y (x × y) = − 60

x = 4 − y

(4 − y)× y = − 60

Desarrollando la ecuación de segundo grado, obtenemos las soluciones x = 10 ; y = − 6, así que los binomios originales serían:

(M + 10) y (M − 6)

Vimos que los binomios pueden representar las magnitudes de longitud y el producto de 2 binomios puede aplicarse al cálculo del área de un cuadrado y, en esta oportunidad, de un rectángulo. Las Matemáticas siguen siendo la base fundamental para las ciencias aplicadas y la formulación de expresiones que facilitan el cálculo de magnitudes susceptibles a ser medidas. Para aclarar, cuando me refiero al "cálculo binomial" es por la utilización de binomios en un cálculo algebraico.+

Apoyo bibliográfico y fuente de imágenes

Nuestra lógica y razonamiento matemático pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de jcoope12: Portada sobre Cálculo Binomial
• Youtube: Perímetro y área
• Blog: Factorización de trinomios
• Blog: Las identidades notables

Las identidades matemáticas son expresiones algebraicas
que facilitan el cálculo de magnitudes susceptibles
a ser medidas, como el área de un terreno o una figura geométrica