Saludos de nuevo mis queridos amigos espero que se encuentren todos muy bien, especialmente la comunidad de @Cervantes, muchos son los fenómenos que se desarrollan a nuestro alrededor, siendo uno de ellos, el sonido, en esta oportunidad analizare algunas variables de dicho fenómeno, como notable ejemplo del movimiento ondulatorio, en pasadas entregas he podido analizar cualquier tipo de movimiento, incluyendo el ondulatorio, pero, ahora lo quiero hacer resolviendo ejercicios aplicando las respectivas fórmulas matemáticas al respecto.

Antes de comenzar con el propósito planteado, podemos recordar la trayectoria de un movimiento ondulatorio, señalando su longitud de ondas y, amplitud de la misma, como pueden ver a continuación en la siguiente figura 1.

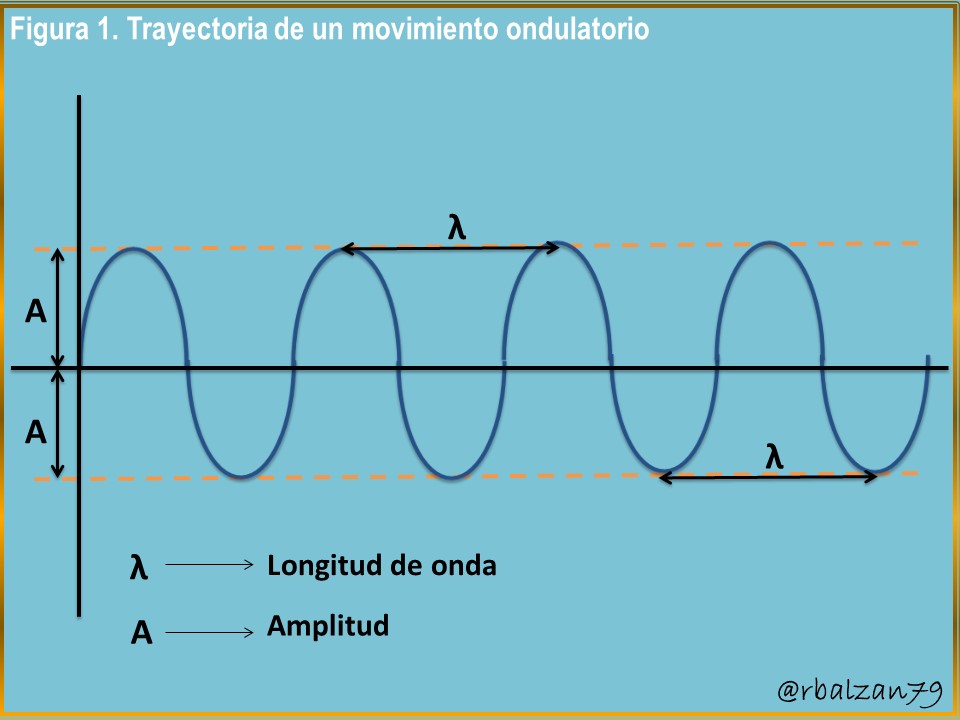
Con la anterior figura 1 nos comenzamos a relacionar con dos magnitudes física vinculadas con un movimiento ondulatorio, la longitud de onda y amplitud, por ejemplo, el sonido. Las ondas son perturbaciones que se propagan a través de determinado medio material o elástico, como el aire, ahora es conveniente introducir otra magnitud como la frecuencia de oscilación de estas ondas, en este caso, ondas sonoras.

Donde T constituye el tiempo implementado por un determinado punto de la onda en recorrer un ciclo completo. Ahora visualicemos la fórmula de longitud de onda.

Esta magnitud física representa la distancia o longitud entre dos puntos consecutivos de dicha onda analizada. En relación a su velocidad de propagación tenemos la siguiente fórmula.

La velocidad de propagación representa la rapidez con la cual se desplaza una señal acústica o frente de onda, de esta manera, ya se ha identificado cada una de las fórmulas a utilizar en el siguiente planteamiento.

Ejercicio

Tenemos un diapasón el cual lo hemos golpeado con otro material metálico, debido a esta acción emitimos un sonido, haciendo que el diapasón vibre a 150 Hz (Hertz), considerando la velocidad del sonido en 340 m/s en el medio material como el aire, calcular lo siguiente:

a.- Cual será la longitud de onda de dicho sonido.

b.- Calcular su período de oscilación completa.

c.- Que tiempo implementará dicho sonido al recorrer 50 veces su longitud de onda.

Datos:
v= 340 m/s.
f= 150 Hz.

Solución

a.- Comenzaremos utilizando la fórmula (3) v= ʎ.f, nos queda:

b.- Para responder a esta incógnita, tenemos que el período de una oscilación completa (T) es inversamente proporcional a su frecuencia, entonces, de la fórmula 1, obtenemos lo siguiente:

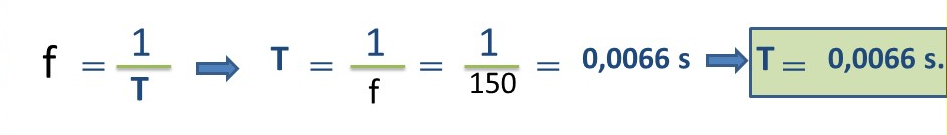
c.- Con el cálculo de la longitud de onda, nos queda realizar el siguiente producto:

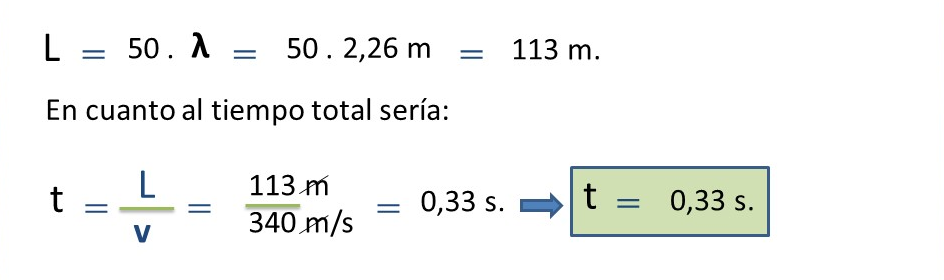
De esta manera se ha resuelto las tres interrogantes planteadas, donde se obtuvo la longitud de onda (ʎ) del sonido emitido, el tiempo de su oscilación completa (T), y la longitud y tiempo total cuando dicho sonido recorrió 50 veces su propia longitud de onda.

Hasta otra oportunidad mis queridos amigos.

Nota: Las imágenes fueron realizadas por el autor utilizando Power Point.

Referencia Bibliográfica recomendada

[1] MOVIMIENTO ONDULATORIO. Link.