Finding Area of Triangle |Only Lengths of Medians are Given

Hello math bugs(🐞) and hivers(🐝)
I hope you are doing well in life.

Welcome to another episode of gemeteic problem and it's sulution. We allready know how to find the area of a triangle when sides are given. We use heron's formulla to find it out. Today we will get to know how area of a triangle related to its median, how area can be obtain from given medians. In case you, if you don't know, let me introduce you with the medians of a triangle.

A triangle has three vertices and three sides. When we draw a straight line from a vertex of a trinagle to join it to the mid point of its opposite side, we get a median. Thus when we connect three pair of dots from three vertices to mid points of opposite sides of a triangle, we get three medians. In the figure below, you see three of ∆ABC i.e AD, BE and CF.

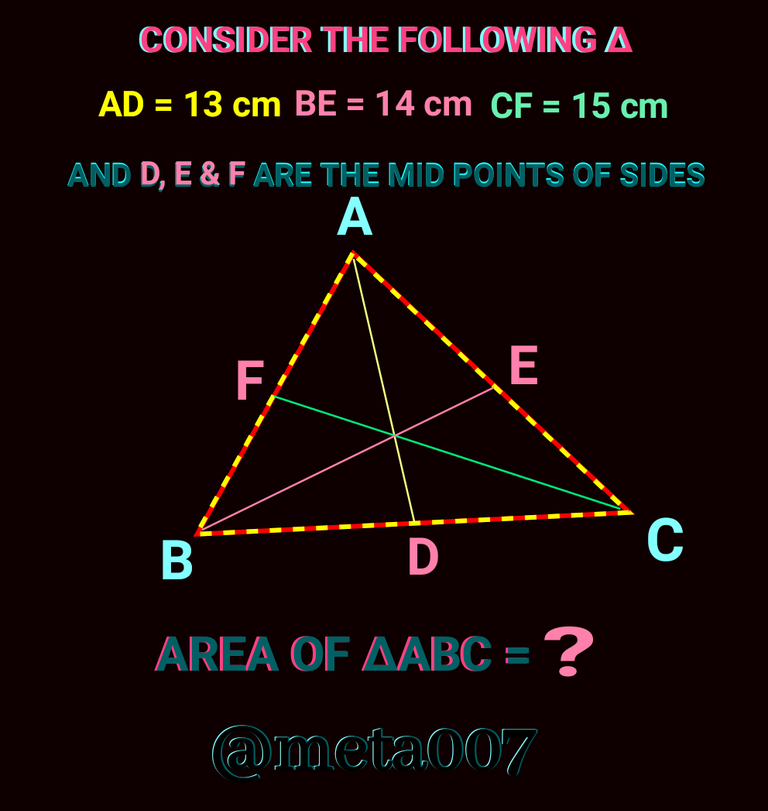
If we know the measurement of three medians of a triangle we can easily obtain its area. Which can simply given by 4/3 of area of the triangle made by medians AD, BF & CF or Ar.∆ABC = 4/3( area formed by considering AD, BE & CF). Check the following figure for better understanding.

Now check the solution:

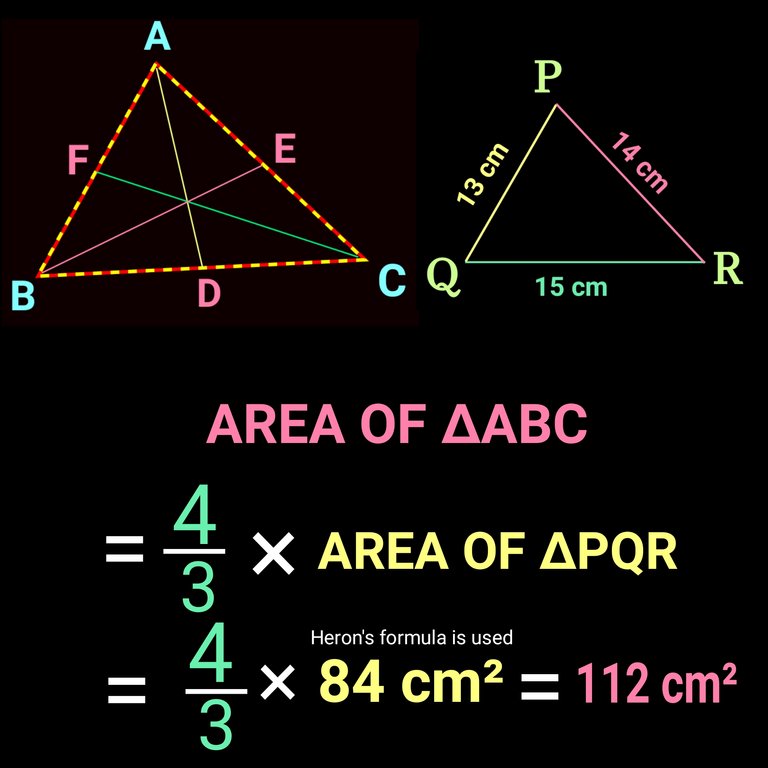
Actually I lied to you. I haven't used any formula right now. The area is crammed. To tell the truth the Cir-cum-raidus and in-radius of triangle ∆PRQ are also crammed ..lol R= 4 cm and r= 1 cm.. 😆 You can use heron's formula to varify. Who knows I can be wrong as I haven't calculated it now.

You can check Heron's formula to know how it works explained in previous post.

You must know the formula (ar.∆ABC =4/3× ar.∆PQR) discissd above to get to answer. But how??

Before heading to proof, we need to know a few facts but we can't prove it here. All proofs at the same time, will make the explanation abracadabra and will alos make you confused. So , I'll just mention the facts, so that we fetch no problem while we try to prove it.

Fact one: the point centroid is found joining the mid points of sides to its opposite vertices.

Fact two: A Centroid always divides a median in 2:1 ratio as we can see in the following figure.

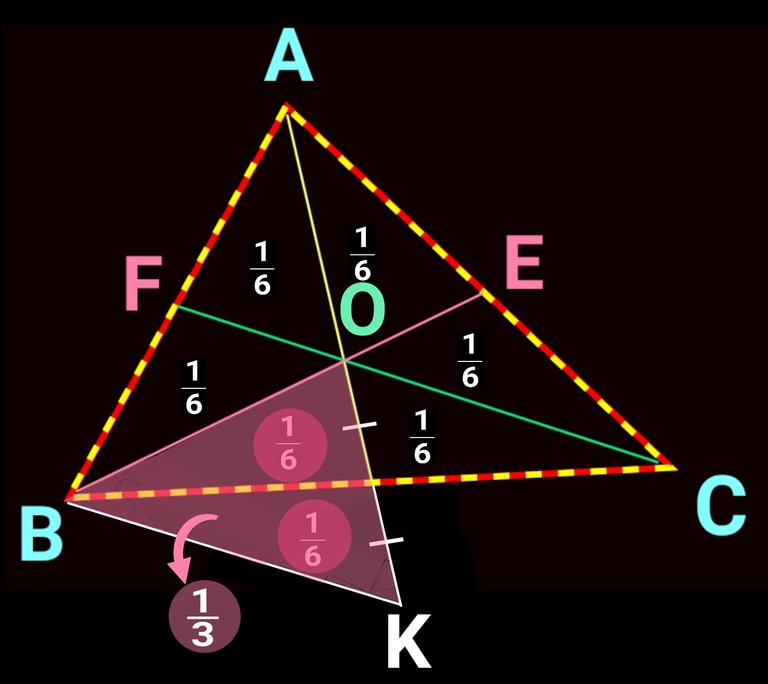
Fact three: All three centroids divide a triangle in 6 equal segment. In the following figure smaller trinagles inside ∆ABC are equal in their area.

For details you may check Centroid/Geocentre in my previous post.

Let's prove it

We need a little bit of construction here. Let's do it first, check it in the following figure.

As, we already know that all the smaller triangle in side ∆ABC have equal area i.e. ar.(∆AFO = ∆BFO = ∆BDO = ∆CDO = ∆CEO = ∆AEO). We can also say that area of each of them is one-sixth of ∆ABC.

Now consider ∆CDO and ∆BDK:

1) OD = KD [ As per construction]
2) BD = CD [ A median touches mid point of side]
3) ∠BDK = ∠CDO [ Vertically opposite angles are equal]

As per S-A-S property of congruency ∆CDO ≅ ∆BDK.

So, area of triangle ∆CDO & ∆BDK are equal. Each of them got one-sixth of ∆ABC.

Look at ∆BOK

ar.∆BOK = ar.∆BOD + ar.∆BKD

Or, ar.∆BOK = 1/6 area of ∆ABC + 1/6 area of ∆ABC

Or, ar.∆BOK = 1/3 area of ∆ABC

Now look at the following figure:

Let's now compute the required formula. We will start from ar.∆BOK= 1/3 area of ∆ABC. Let's check the figure below👇

Let's check how semi-perimeter(S) of ∆ABC becomes 2/3 of semi-preimeter(Sₘ) of ∆BOK..👇

Let's go to the final figure, it's almost done👇

In the above figure, I took a few short cut calculation. You may think where 4/9 comes from. You can see inside squre root there are four 2/3. Of four 2/3 comes out of square root, we left by only two of them. That is why I just wrote 4/9. You can see, I was out of space.

Uff... Making all those figures was really a hard work..

📢 All the figures are used in the post are made by me. Figures used here may not be acurate in measurement, so please try considering only given data. Excuess me for silly mistakes if there is any. You may hit a comment or ignore it.

I hope you enjoyed my today's work

Thank you so much for stoping by

Have a nice day

All is well

Regards: @meta007