A problem on angle bisector of a right angle triangle

Hello math bugs(🐞) and hivers(🐝)
I hope you are strong and stout & doing good in life.

Tiady , I have come up with another interesting triangle (∆ABC) problem. There is a right angle triangle. The right angle(90°) is at point B.The bisectors of other two angles meet at a point I inside the triangle. If the perpendiluar on AC from point I is 4 cm, you need to find the lenght of IB. Check it the follwoing figure.

Give it a try first. Then check my solution.

First, let me point out what concept(s)/postulate(s)/ axiom(s) we need to solve it. In my previous post, I have dealth with all of them except a new concept. Let me put them together.

✅ Angle bisectors of a triangle always meet a point inside the trianglel. The point is called in-centre and distance from that point to the sides is called in-radius. Of course the lenghts are same as they are radius of same cricle. Check it in the following figure.

Check details of In-centre

✅✅ The most important point is when two line segments are perpendicular to each other, if another two perpendicular line segments make a quadrilateral with them, it always be an square. Check below what I meant.

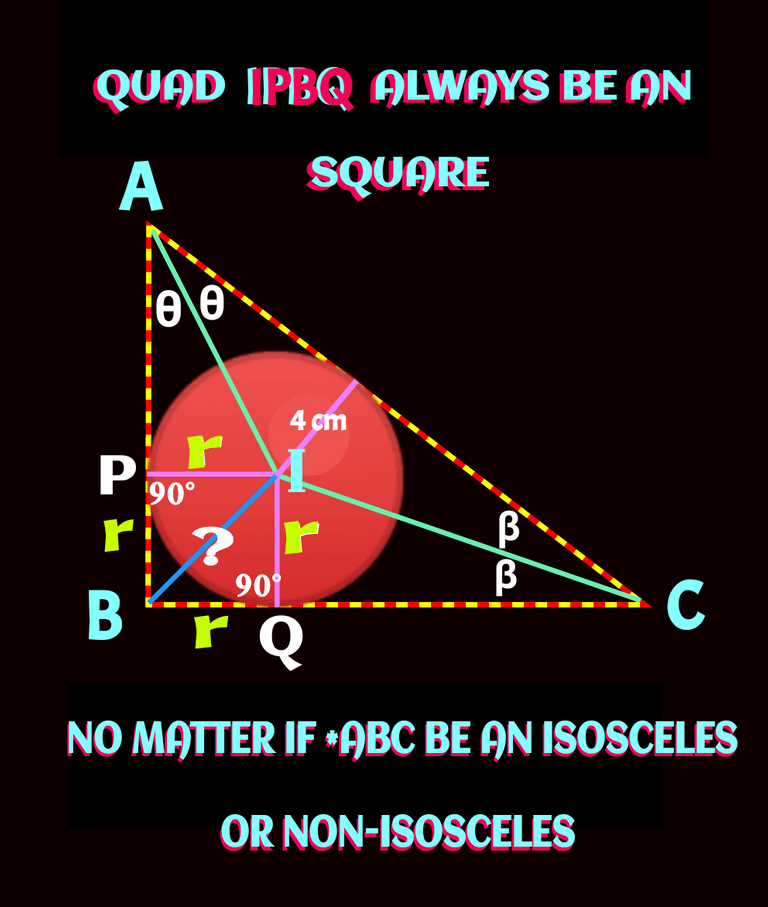
Note: From in-centre two radius drawn to the perpendicular sides of a right angle triangle , always make an square (⬛). No matter what kind of right triangle it is.

✅✅✅ The 3rd point is an easy one. We need to find out the lenght of a diagonal the the square. Here in the problem it will IB. Check it below

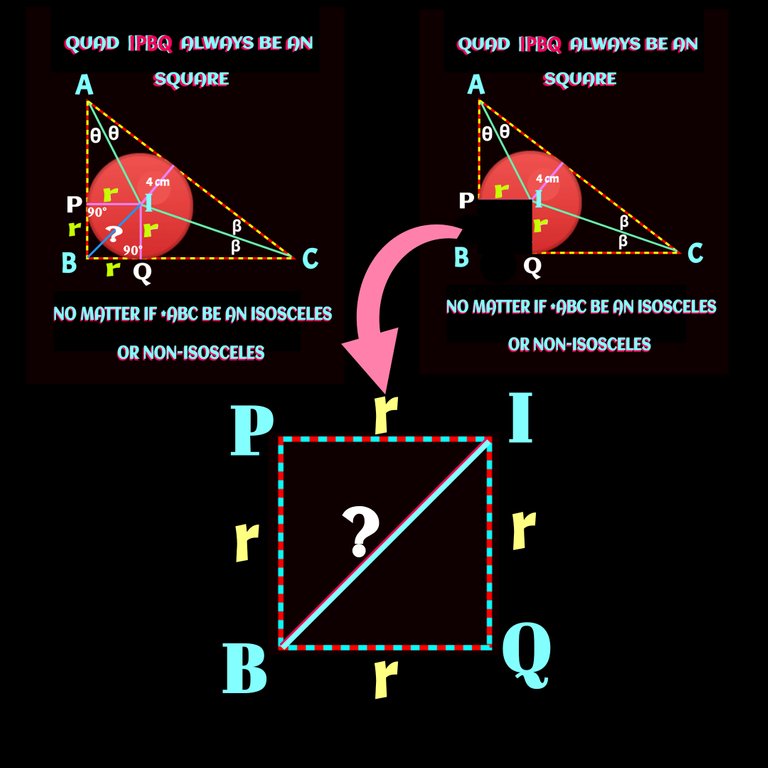
If you got these three points, problem will be as easy a eating a sweet cake. (🍰)

SOLUTION:

Now nothing left to solve. Still I'll solve it for you😄. We already know how to find a diaginal. It is a√2 unit where a is the side of the square. Check it 👇

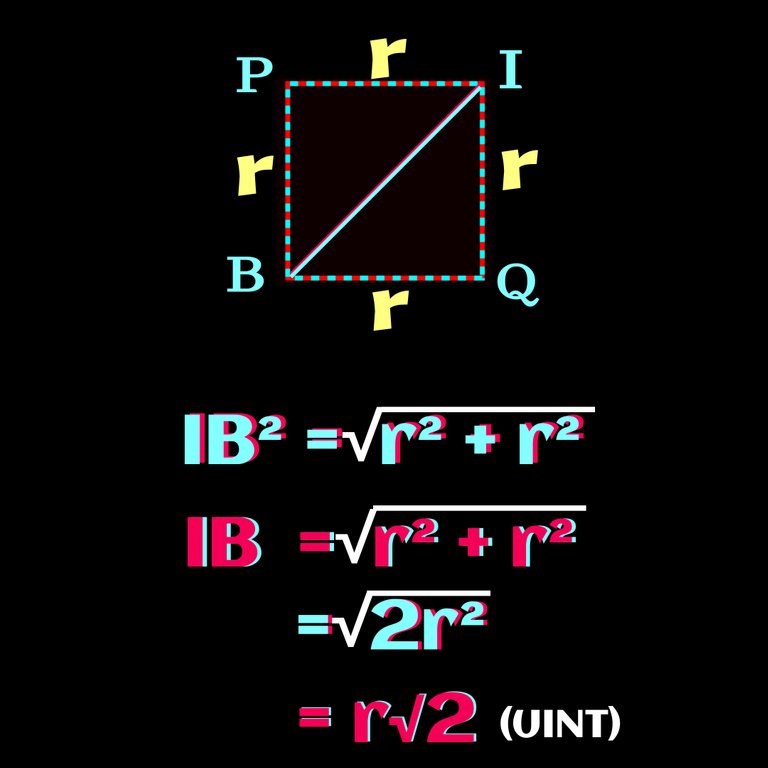
Hecne , the required lentgh be
IB = r√2 unit
So, IB =4√2 cm.

All the pics/figures used are made by me. The drawing I made may not be accurate in messurement. So, I request you to consider the info given only. There may be some silly mistakes while typing or making those figures. Please ingore them if there is any.

I hope you liked my presentention of Today's problem.

Thank you so much for visiting

Have a nice day

All is well

Regards: @meta007