Research diaries #12: Berkin's paradox and why the worst restaurants are in the most touristy spots

Lately I have been delving a bit into statistics. Today we will be looking at a famous paradox about why correlation does not have to imply causation.

Source Pixabay license by Dimhou

Let me sketch the scene. Your average touristy capital, like Amsterdam, is covered with overpriced bad restaurants at its best locations. Their price to quality ratio might make you suspect that these places almost close as quickly as they open. But no, quite a lot of these seem to survive from the flow of tourists which covers their extreme rent ( I am thinking about a pre-covid lockdown world:P). On the other spectrum of restaurants that have been open for a long time we have local restaurants with great food. They are quite often tucked away in alleys hidden from tourists. They have a large regular customer base and don't have such high costs as they are located in the not so popular places so their rent is much lower.

Here is the main question: can we conclude that food-quality is causally related to how touristy a restaurant is?

Just to make it clear the question arises from an observed correlation. We want somehow see if such an correlation always implies causation.

We tackle the problem by defining a statistical model. So we need to define variables. We will keep it simple and just consider two: food-quality score and tourist score. The score range can be positive or negative but the greater the better. So a restaurant with tourist score 3 is very touristic compared to a restaurant with tourist score -3. These two variables will be chosen randomly and independently from each other. Then we need to define a survivability score which we will just take equal to the food quality score + tourist score. The restaurants that survive must have a score that is in the top 10% (I am not sure if the real world is that bad but it won't matter much for the results).

Before we continue realize that in this model there is no dependency between the food quality score and the tourist score. This means that this model assumes there is no causation. The question is now if we can still observe the correlation that that the more touristy a place is the more crap the food is. If this is the case then we cannot conclude that there is any causation.

So what do we get if we run this with normal distributions:

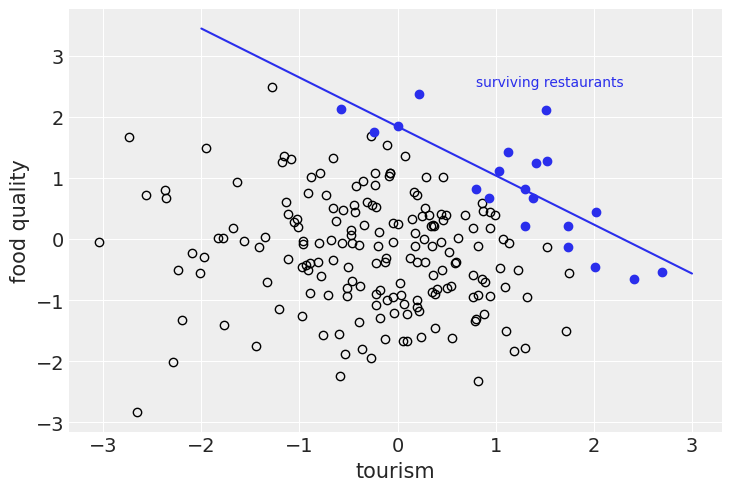
The blue points are the surviving restaurant and the blue line is a linear curve that we regressed through the blue points. Behold that we observe the correlation!

So what is this phenomenon. It is is called Berkin's paradox and it is a feature of the independent variables which can lead to a false causation.

To make it a bit more clearer we can visualize the model as a nice graph. Here the food and tourist score both influence the survival of a restaurant so we get the following connections:

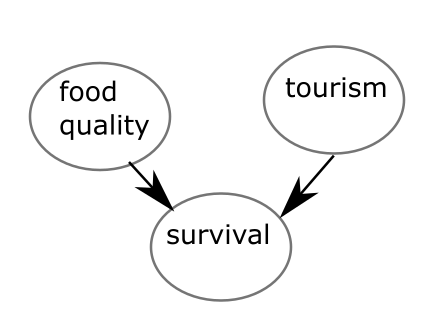
But there is no connection between the food and tourist score. Hence, there is no causation.

References: This lovely example was taken from Statistical Rethinking from McElreath. He does it with research grants and trustworthiness versus newsworthiness but it is the same idea. The book is a great read as an introduction to Bayesian modelling.