Hydrogen- the most abundant element in the universe! -Part 13-

Treatment of the dihydrogen(+) ion by the LCAO method:

For the study of molecules with multiple electrons, there are a number of approximation techniques that result in molecular orbitals because the calculation techniques no longer allow for the strict solution of the Schrodinger equation. We will select the general method out of these approximation techniques: LCAO (Linear Combinations of Atomic Orbitals).
An electron is essentially only subjected to the attraction of the nucleus it is passing near when doing so. As a result, the electron in a molecule located close to the nuclei is roughly described by the same atomic orbital that would describe the electron in an isolated atom. So, it is possible to build molecular orbitals using the hydrogen ψ1s atomic orbitals as a starting point.

Views in three dimensions of atomic orbitals that resemble hydrogen that display probability density and phase- Wikipedia
The wave function ϕ, which describes the electron in H2(+), will therefore be assumed to be a linear combination of the atomic orbitals ψA and ψB of two isolated hydrogen atoms, A and B:
ϕ= CA ΨA+ CB ΨB (The actual coefficients CA and CB must be calculated because they are unknown.)

• A 1s atomic orbital corresponds to each of the functions ΨA and ΨB.

Schrodinger's equation will be expressed as follows:
Hϕ = Eϕ (E is the molecular ion's electron energy, and H is its monoelectric Hamiltonian)
Integrate over the entire space after multiplying both sides of the equation by the ϕ function:

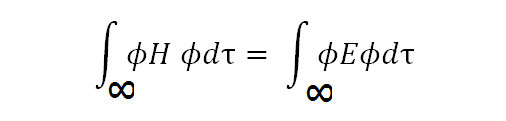
[Created by using word microsoft]

Let it be:

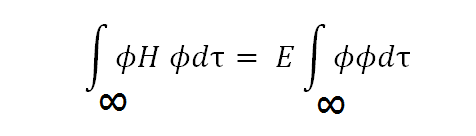
[Created by using word microsoft]

Given that E is a constant, where:
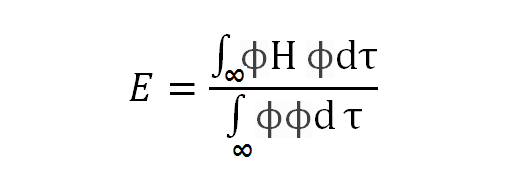(1)
[Created by using word microsoft]

E is a function of the unidentified coefficients CA and CB, according to Relation (1). Due to the requirement that the discovered molecular states be stable states, the best values for the coefficients CA and CB will be those that minimize the energy E.
The energy level that results from the linear combination of ΨA and ψB is lower than the energy level of the hydrogen atoms considered separately. With regard to CA and CB, the extremum of E will be a minimum, and the following mathematical condition will be written:

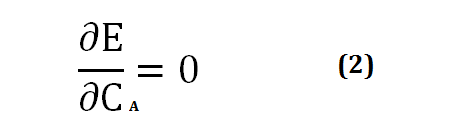
[Created by using word microsoft]

and:

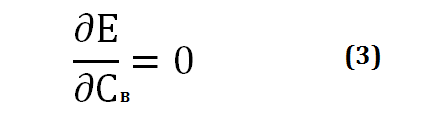
[Created by using word microsoft]

The ratio CA/CB and the energy E can be obtained by solving the system of equations (2) and (3), which are homogeneous and linear in CA and CB. Two values of the CA/CB ratio are obtained from this calculation, known as the calculation of variations:
CA/CB= +1
CA/CB= -1
therefore, two wave functions:
ϕ+ = CA (ΨA + ψB) and ϕ- = CA (ΨA - ψB)
The normalization condition is expressed as follows:
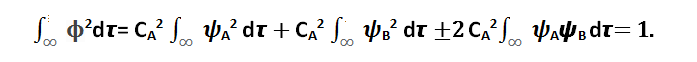(4)
[Created by using word microsoft]

Atomic orbitals ΨA and ψB have already undergone normalization:

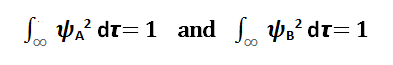
[Created by using word microsoft]

The amount of overlap between the ΨA and ψB orbitals is measured by the covering integral
The overlap zone is the collection of points shared by the two orbitals; the larger this area, the higher the value of S.

• Then it is written as Equation (4):
  
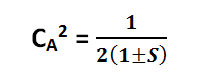
  [Created by using word microsoft]

These are the molecular orbitals:

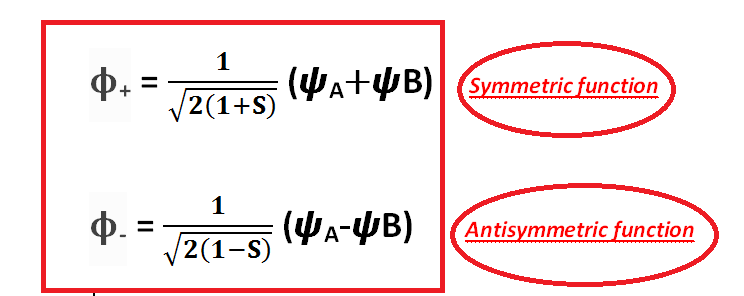
[Created by using word microsoft]

Bibliographic references:

• [General and inorganic chemistry book- M. Shkhashirou- H. Birqdad- Y. Qodsi- University publications. Algeria]

• Hydrogen- Wikipedia

• Atome d'hydrogène- Wikipedia

• Acids, bases, pH, and buffers- Khan academy

• [Smail Meziane: Livre Chimie générale- Structure de la matiére. Berti edition, Alger, 2006]

• [Livre- Chimie génerale- R.Ouahes]

• ÉNERGIE DE L'ION H2+ PAR LA MÉTHODE LCAO-Michael J. S. Dewor and J6zsef Kelemen

• Linear combination of atomic orbitals